Practice quiz 3

Not graded, just practice

Model fitting

1. True or false, gradient descent and orinary least squares are both iterative optimization algorithms.

True False

2. What cost function have we been using to perform our gradient descent?

standard deviation bootstrapping sum of squared error absolute error

3. True or false, when performing gradient descent on the model given by the equation \(y = w_0 + w_1x_1 + w_2x_2\), we might arrive at a local minimum and miss the global one.

True False

4. Which of the following would work to estimate the free parameters of a nonlinear model?

gradient descent ordinary least squares solution both work

5. True or false, in gradient descent, we search through all possible parameters in the parameter space.

True False

Model fitting in R

Questions 6-9 refer to the code and output below, performing gradient descent with optimg:

optimg(data = data, par = c(0,0), fn=SSE, method = "STGD")

$par
[1] 3.37930046 0.06683237

$value
[1] 959.4293

$counts
[1] 6

$convergence
[1] 0

6. How many steps did the gradient descent algorithm take?

7. What was the sum of squared error of the optimal paramters?

8. What coefficients does the algorithm converge on?

3.37930046, 0.06683237 0, 0 959.4293 6, 0 all of the above

9. What parameters were used to initialized the algorithm?

3.37930046, 0.06683237 0, 0 959.4293 6, 0

Questions 10-12 refer to the output below from lm():

Call:
lm(formula = y ~ x, data = data)

Coefficients:
(Intercept)            x  
    3.37822      0.06688  

10. Use R notation to write the model specification.

answer

y ~ x  # this works (implicit intercept)

y ~ 1 + x # this also works (explicit intercept)

11. Given the model is specified by the equation \(y = w_0+w_1x_1\), what is the parameter estimate for \(w_0\) = and \(w_1\) = .

12. True or false, for this model, optimg() with gradient descent would converge on the same parameter estimates?

True False

Model accuracy

Question 13 refers to the following figure:

13. In the figure above, which of the following corresponds to the residuals?

blue line red lines black dots none of the above

14. Suppose the \(R^2\) value on the model in the figure above is about 0.88. Given this value, which of the following best describes the accuracy of the model?

fairly high accuracy fairly low accuracy not enough information

15. Suppose 0.88 reflects the \(R^2\) for our fitted model on our sample. Which of the following is true about the \(R^2\) for our fitted model on the population?

tends to be higher tends to be lower the same

16. Which of the following best describes an overfit model?

performs well predicting new values, but poorly on the sample performs well on the sample, but poorly predicting new values performs poorly both on the sample and predicting new values performs well both on the sample and predicting new values

17. How can we estimate \(R^2\) on the population? Choose all that apply.

cross validation bootstrapping set.seed none of the above

18. Fill in the blanks below to best describe cross validation:
    • Leave some out
    • Fit a model on the data left outkept in
    • Evaluate the mdoel on the data left outkept in

Model accuracy in R

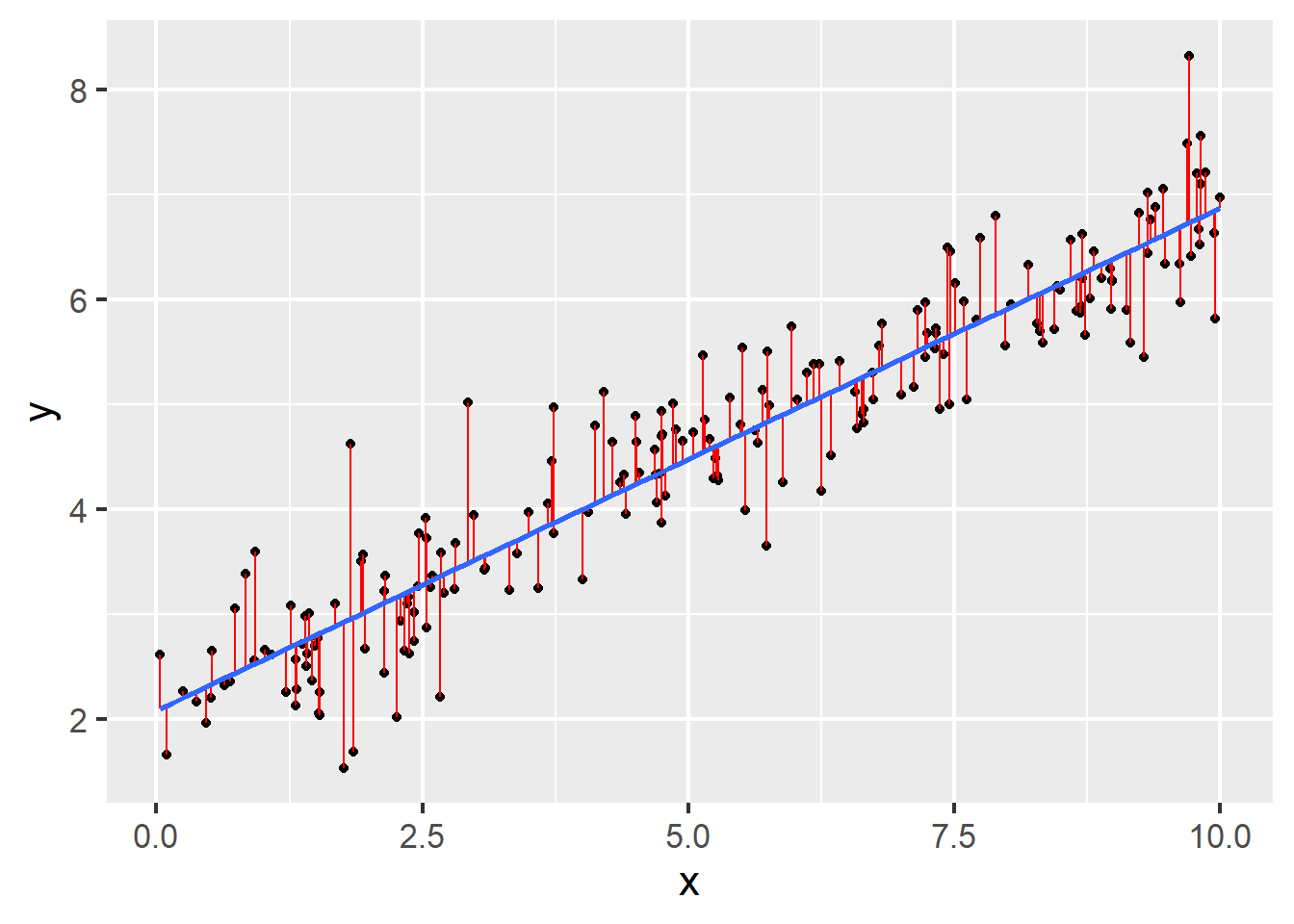
Questions 19-20 refer to the following code and output:

model <- lm(y ~ 1 + x, data)
summary(model)

Call:
lm(formula = y ~ 1 + x, data = data)

Residuals:
     Min       1Q   Median       3Q      Max 
-1.38959 -0.32626 -0.04605  0.31967  1.65977 

Coefficients:
            Estimate Std. Error t value Pr(>|t|)    
(Intercept)  2.08280    0.07418   28.08   <2e-16 ***
x            0.47844    0.01242   38.51   <2e-16 ***
---
Signif. codes:  0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1

Residual standard error: 0.5139 on 198 degrees of freedom
Multiple R-squared:  0.8822,    Adjusted R-squared:  0.8816 
F-statistic:  1483 on 1 and 198 DF,  p-value: < 2.2e-16

19. What is the \(R^2\) value for the model fit above?

20. Does the value you entered in 19 reflect \(R^2\) on the population or on the sample?

population sample

Questions 21-23 refer to the following code and output:

# we divide the data into v folds for cross-validation
set.seed(2) 
splits <- vfold_cv(data)

# model secification 
model_spec <- 
  linear_reg() %>%  
  set_engine(engine = "lm")  

# add a workflow
our_workflow <- 
  workflow() %>%
  add_model(model_spec) %>%  
  add_formula(y ~ x) 

# fit models to our folds 
fitted_models <- 
  fit_resamples(
    object = our_workflow, 
    resamples = splits
    ) 

fitted_models %>%
    collect_metrics()

# A tibble: 2 × 6
  .metric .estimator  mean     n std_err .config             
  <chr>   <chr>      <dbl> <int>   <dbl> <chr>               
1 rmse    standard   0.507    10  0.0397 Preprocessor1_Model1
2 rsq     standard   0.890    10  0.0146 Preprocessor1_Model1

21. In the cross-validation performed above, how many folds were the data split into?

2 5 10

22. What \(R^2\) do we estimate for the population?

23. What model has been fit?

y ~ x y ~ x^2 x ~ y vfold_cv

Questions 24-26 refer to the following code and output:

# we bootstrap the data for cross-validation
set.seed(2) 
bootstrap <- bootstraps(data) 

# fit models to our folds 
fitted_models_boot <- 
  fit_resamples(
    object = our_workflow, 
    resamples = bootstrap
    ) 

fitted_models_boot %>%
    collect_metrics()

# A tibble: 2 × 6
  .metric .estimator  mean     n std_err .config             
  <chr>   <chr>      <dbl> <int>   <dbl> <chr>               
1 rmse    standard   0.507    25 0.00946 Preprocessor1_Model1
2 rsq     standard   0.887    25 0.00377 Preprocessor1_Model1

24. How many bootstrap samples did we generate?

25. True or false, we fit the same model to the bootstrap data as we did in the cross-validation code.

TRUE FALSE

26. True or false, the \(R^2\) estimated by bootstrapping is equal to the \(R^2\) estimated by cross-validation.

TRUE FALSE