Model Accuracy

Data Science for Studying Language and the Mind

Katie Schuler

2023-10-24

You are not alone

by Allison Horst

You are `here`

Data science with R

Hello, world!
R basics
Data importing
Data visualization
Data wrangling

Stats & Model buidling

Sampling distribution
Hypothesis testing
Model specification
Model fitting
Model accuracy
Model reliability

More advanced

Classification
Feature engineering (preprocessing)
Inference for regression
Mixed-effect models

Model building overview

Model specification: what is the form?
Model fitting: you have the form, how do you guess the free parameters?
Model accuracy: you’ve estimated the parameters, how well does that model describe your data?
Model reliability: when you estimate the parameters, there is some uncertainty on them

Dataset

library(languageR)
glimpse(english)

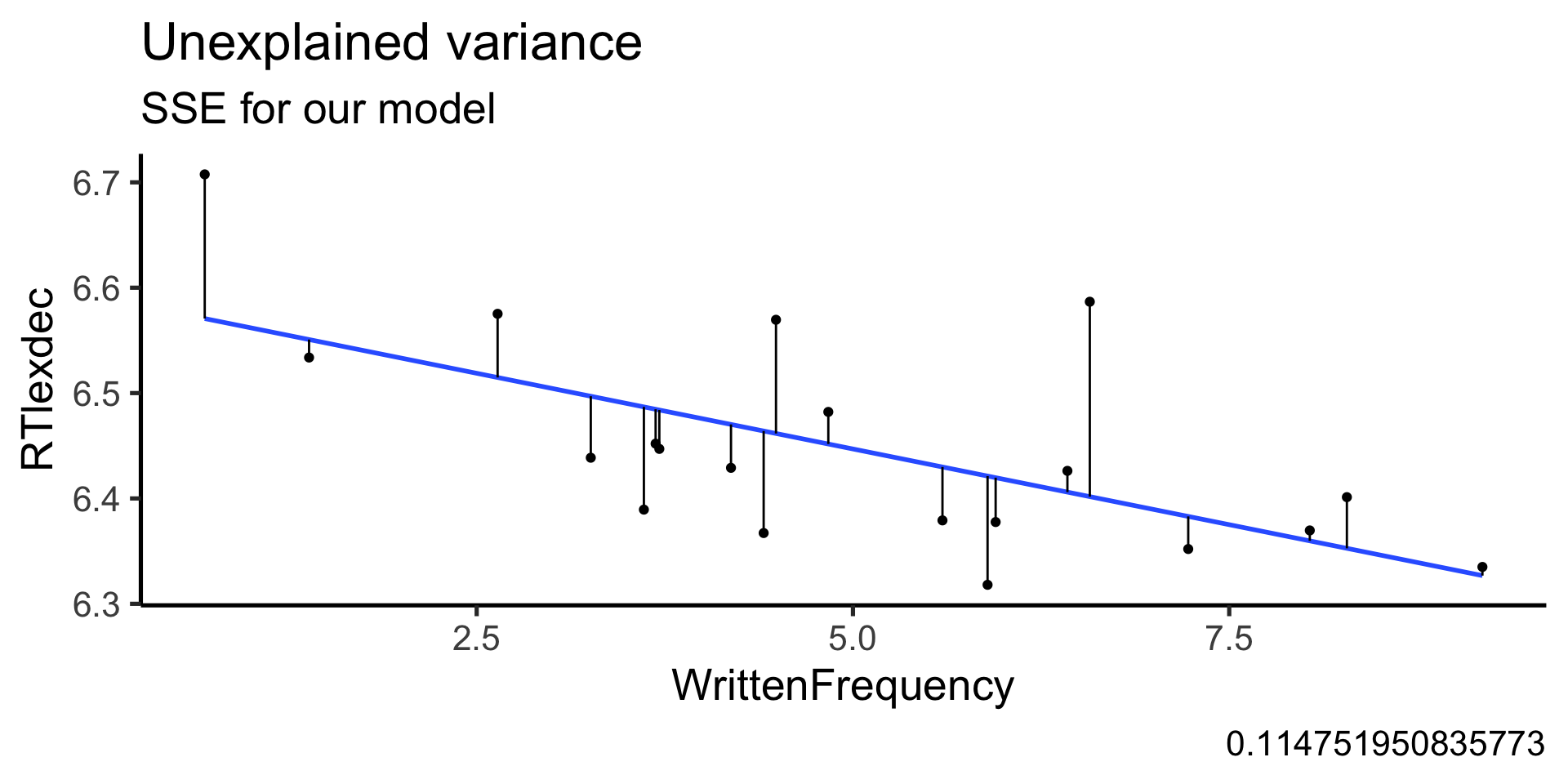
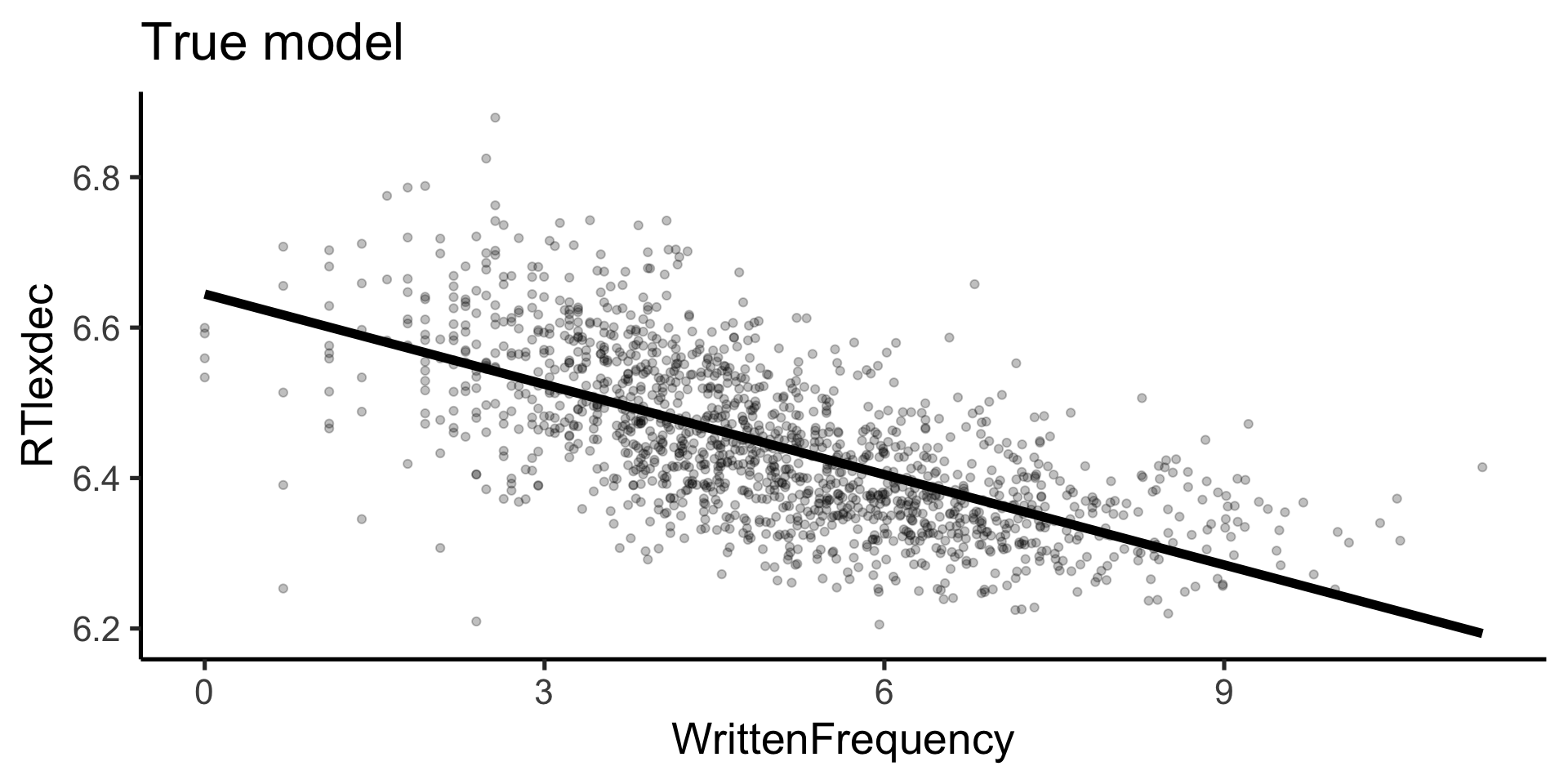
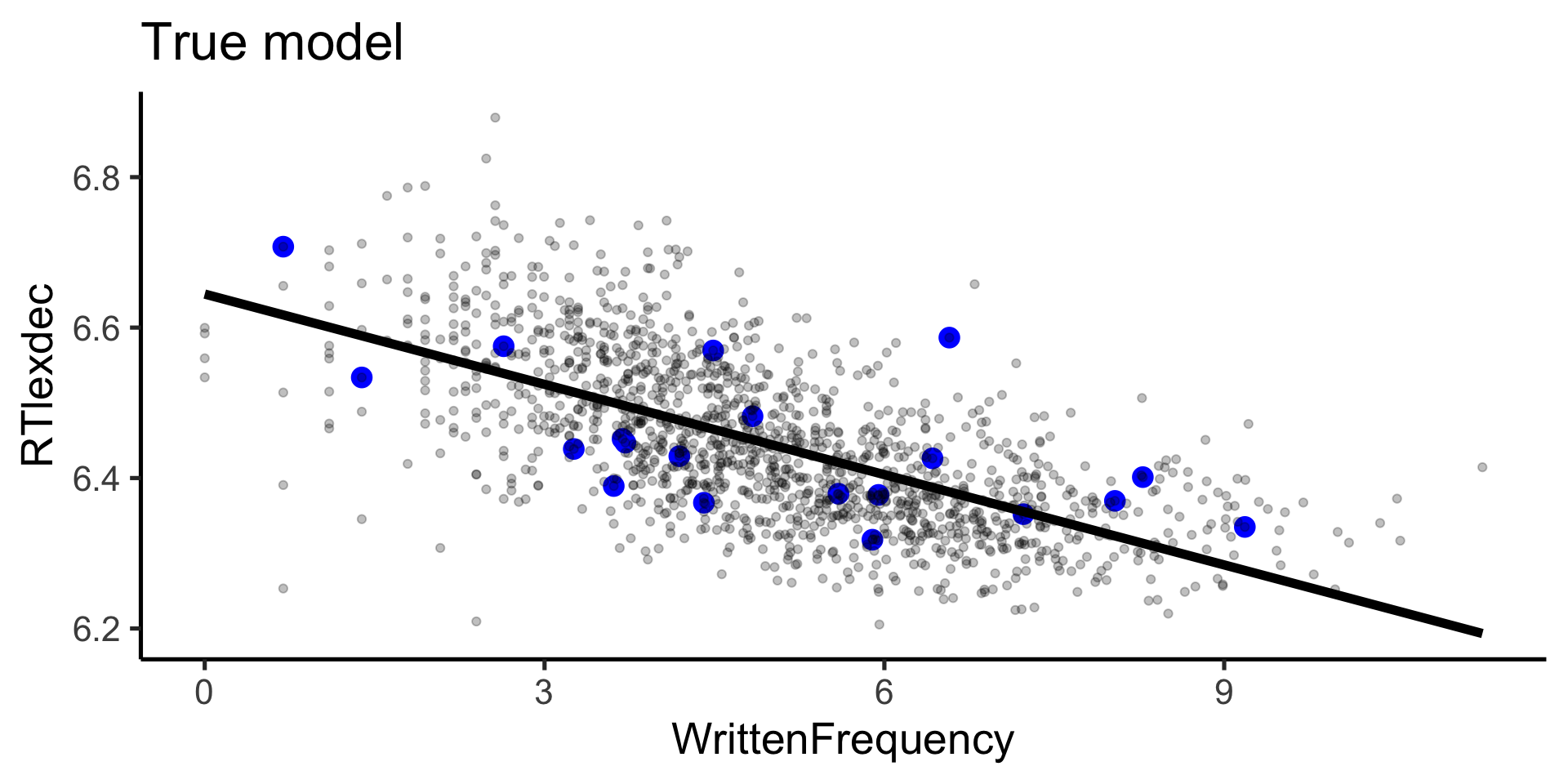
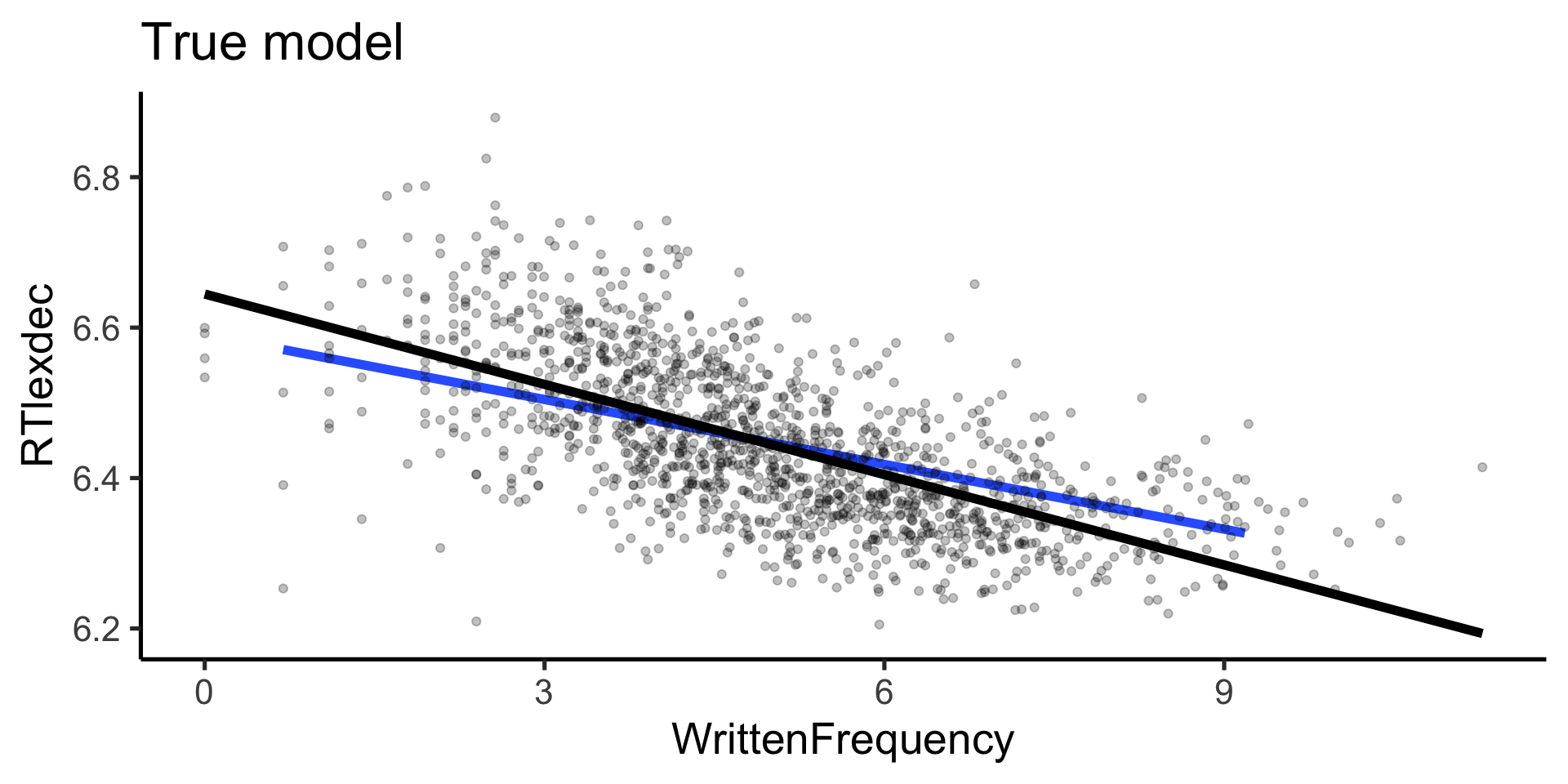
Rows: 4,568
Columns: 36
$ RTlexdec                        <dbl> 6.543754, 6.397596, 6.304942, 6.424221…
$ RTnaming                        <dbl> 6.145044, 6.246882, 6.143756, 6.131878…
$ Familiarity                     <dbl> 2.37, 4.43, 5.60, 3.87, 3.93, 3.27, 3.…
$ Word                            <fct> doe, whore, stress, pork, plug, prop, …
$ AgeSubject                      <fct> young, young, young, young, young, you…
$ WordCategory                    <fct> N, N, N, N, N, N, N, N, N, N, N, N, N,…
$ WrittenFrequency                <dbl> 3.9120230, 4.5217886, 6.5057841, 5.017…
$ WrittenSpokenFrequencyRatio     <dbl> 1.02165125, 0.35048297, 2.08935600, -0…
$ FamilySize                      <dbl> 1.3862944, 1.3862944, 1.6094379, 1.945…
$ DerivationalEntropy             <dbl> 0.14144, 0.42706, 0.06197, 0.43035, 0.…
$ InflectionalEntropy             <dbl> 0.02114, 0.94198, 1.44339, 0.00000, 1.…
$ NumberSimplexSynsets            <dbl> 0.6931472, 1.0986123, 2.4849066, 1.098…
$ NumberComplexSynsets            <dbl> 0.000000, 0.000000, 1.945910, 2.639057…
$ LengthInLetters                 <int> 3, 5, 6, 4, 4, 4, 4, 3, 3, 5, 5, 3, 5,…
$ Ncount                          <int> 8, 5, 0, 8, 3, 9, 6, 13, 3, 3, 1, 9, 1…
$ MeanBigramFrequency             <dbl> 7.036333, 9.537878, 9.883931, 8.309180…
$ FrequencyInitialDiphone         <dbl> 12.02268, 12.59780, 13.30069, 12.07807…
$ ConspelV                        <int> 10, 20, 10, 5, 17, 19, 10, 13, 1, 7, 1…
$ ConspelN                        <dbl> 3.737670, 7.870930, 6.693324, 6.677083…
$ ConphonV                        <int> 41, 38, 13, 6, 17, 21, 13, 7, 11, 14, …
$ ConphonN                        <dbl> 8.837826, 9.775825, 7.040536, 3.828641…
$ ConfriendsV                     <int> 8, 20, 10, 4, 17, 19, 10, 6, 0, 7, 14,…
$ ConfriendsN                     <dbl> 3.295837, 7.870930, 6.693324, 3.526361…
$ ConffV                          <dbl> 0.6931472, 0.0000000, 0.0000000, 0.693…
$ ConffN                          <dbl> 2.7080502, 0.0000000, 0.0000000, 6.634…
$ ConfbV                          <dbl> 3.4965076, 2.9444390, 1.3862944, 1.098…
$ ConfbN                          <dbl> 8.833900, 9.614738, 5.817111, 2.564949…
$ NounFrequency                   <int> 49, 142, 565, 150, 170, 125, 582, 2061…
$ VerbFrequency                   <int> 0, 0, 473, 0, 120, 280, 110, 76, 4, 86…
$ CV                              <fct> C, C, C, C, C, C, C, C, V, C, C, V, C,…
$ Obstruent                       <fct> obst, obst, obst, obst, obst, obst, ob…
$ Frication                       <fct> burst, frication, frication, burst, bu…
$ Voice                           <fct> voiced, voiceless, voiceless, voiceles…
$ FrequencyInitialDiphoneWord     <dbl> 10.129308, 9.054388, 12.422026, 10.048…
$ FrequencyInitialDiphoneSyllable <dbl> 10.409763, 9.148252, 13.127395, 11.003…
$ CorrectLexdec                   <int> 27, 30, 30, 30, 26, 28, 30, 28, 25, 29…

Quantifying model accuracy

We can visualize to get a sense of accuracy
But want to quantify accuracy (determine whether model is useful or how it compares to other models)

Quantifying model accuracy

sum of squared error (depends on units, difficult to interpret)
\(R^2\) (independent of units, easy to interpret)

\(R^2\) quantifies the percentage of variance in the response variable that is explained by the model.

Variance

\(\frac{\sum_{i=1}^n (y_i - m_i)^2}{n-1}\)

We take the sum of squares
square the residuals (\(i^{th}\) data point minus the \(i^{th}\) model value)
then divide by the number of cases, \(n\), minus 1.

Coefficient of determination, \(R^2\)

. . . \(R^2=100\times(1-\frac{unexplained \; variance}{total \; variance})\)

\(R^2=100\times(1-\frac{\sum_{i=1}^n (y_i - m_i)^2}{\sum_{i=1}^n (y_i - \overline{y})^2})\)

\(R^2=100\times(1-\frac{SSE_{model}}{SSE_{reference}})\)

Coefficient of determination, \(R^2\)

\(R^2=100\times(1-\frac{SSE_{model}}{SSE_{reference}})\)

# compute R2 from SSEs
1 - (sse_model/sse_ref)

[1] 0.4081037

# compute R2 from lm
summary(model)


Call:
lm(formula = RTlexdec ~ 1 + WrittenFrequency, data = young_nouns_sample)

Residuals:
     Min       1Q   Median       3Q      Max 
-0.10323 -0.04426 -0.02401  0.03499  0.18496 

Coefficients:
                  Estimate Std. Error t value Pr(>|t|)    
(Intercept)       6.590645   0.044550 147.940  < 2e-16 ***
WrittenFrequency -0.028736   0.008157  -3.523  0.00243 ** 
---
Signif. codes:  0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1

Residual standard error: 0.07984 on 18 degrees of freedom
Multiple R-squared:  0.4081,    Adjusted R-squared:  0.3752 
F-statistic: 12.41 on 1 and 18 DF,  p-value: 0.00243

\(R^2\) overestimates model accuracy

	Population	Sample
True	high	high
Fitted	low	`very high`

Accuracy of the fitted model on the sample overestimates true accuracy of fitted model.

Overfitting

You have the freedom to fit your sample data better and better (you can add more and more terms, increasing the \(R^2\) value). But be careful not to fit the sample data too well.

any given set of data contains not only the true model (signal), but also random variation (noise).
Fitting the sample data too well means we fit not only the signal but also the noise in the data.
An overfit model will perform really well on the data it has been trained on (the sample), but would predict new, unseen values poorly.
Our goal is to find the optimal fitted model – the one that gets as close to the true model as possible without overfitting.

Cross-validation justificaiton

We want to know: how well does the model we fit describe the population we are interested in.
But we only have the sample, and \(R^2\) on the sample will tend to overestimate the model’s accuracy on the population.
To estimate the accuracy of the model on the population, we can use cross-validation

Cross-validation steps

Given a sample of data, there are 3 simple steps to any cross-validation technique:

Leave some data out
Fit a model (to the data kept in)
Evaluate the model on the left out data (e.g. \(R^2\))

There are many ways to do cross-validation — reflecting that there are many ways we can leave some data out — but they all follow this general 3-step process.

Two common cross-validation approaches

In leave-one-out cross-validation, we leave out a single data point and use the fitted model to predict that single point. We repeat this process for every data point, then evaluate each model’s prediction on the left out points (we can use \(R^2\)!).
In k-fold cross-validation, instead of leaving out a single data point, we randomly divide the dataset into \(k\) parts and use the fitted model to predict that part. We repeat this process for every part, then evaluate each model’s prediction on the left out parts (again, we can use \(R^2\)!).