
Model Fitting
Data Science for Studying Language and the Mind
2024-10-22
Announcements
Final exam scheduled for December 19th at noon
If you have a conflict, please let us know by Demeber 6. We can proctor an earlier date.
Pset 03 solutions to be posted today!
Psets 04 and 05 pushed back by one week
You are here
Data science with R
- R basics
- Data visualization
- Data wrangling
Stats & Model building
- Sampling distribution
- Hypothesis testing
- Model specification
Model fitting- Model accuracy
- Model reliability
More advanced
- Classification
- Inference for regression
- Mixed-effect models
Roadmap
- Fitting linear models in R
- Goodness of fit: quantifying our intuition
- Search problem: How do we find the best one?
- Gradient descent - iterative optimization algorithm
- Ordinary least squares - analytical solution for linear regression
- If time: another full example
Fit a linear model
| model specification | |
|---|---|
| R syntax | rt ~ 1 + experience |
| R syntax | rt ~ experience |
| Equation | \(y=w_0+w_1x_1\) |
\(y = 211.271 + -1.695x\)
Fit a linear model in R

| model specification | |
|---|---|
| R syntax | rt ~ 1 + experience |
| R syntax | rt ~ experience |
| Equation | \(y=w_0+w_1x_1\) |
Fitting by intuition
How would you draw a “best fit” line?

- Draw a straight line that goes through as many points as possible.
Fitting by intuition
Which line fits best? How can you tell?


- B, because the model is closer to the data (closer to more of the points)
Quantifying “goodness” of fit
We can measure how close the model is to the data


- We call these the “errors” or “residuals”. We want a single number that would represent goodness of fit.
Sum of squared error
We can quantify our intutition and express goodness of fit with sum of squared error.

| experience | rt | prediction | error | squared_error |
|---|---|---|---|---|
| 49 | 124 | 128.22414 | 4.2241379 | 17.8433413 |
| 69 | 95 | 94.32759 | -0.6724138 | 0.4521403 |
| 89 | 71 | 60.43103 | -10.5689655 | 111.7030321 |
| 99 | 45 | 43.48276 | -1.5172414 | 2.3020214 |
| 109 | 18 | 26.53448 | 8.5344828 | 72.8373960 |
[1] 205.1379\(SSE=\sum_{i=i}^{n} (d_{i} - m_{i})^2 = 205.1379\)
Sum of squared error
\(SSE=\sum_{i=i}^{n} (d_{i} - m_{i})^2\)
Given some data:
| experience | rt | prediction | error | squared_error |
|---|---|---|---|---|
| 49 | 124 | 128.22414 | 4.2241379 | 17.8433413 |
| 69 | 95 | 94.32759 | -0.6724138 | 0.4521403 |
| 89 | 71 | 60.43103 | -10.5689655 | 111.7030321 |
| 99 | 45 | 43.48276 | -1.5172414 | 2.3020214 |
| 109 | 18 | 26.53448 | 8.5344828 | 72.8373960 |
Compute the sum of squared error:
Problem 1: check model parameters
- The
predict()way uses a fitted model, which already has the best fitting free parameters. - We need a way to check different potential model fits to see which one is best.
- Let’s write a function!
Now we can check any model parameters.
Problem 2: yikes
- That’s a lot of parameters to test! (
Inf?) - Also, how do we know when to stop?
Simplests possible case is hard
Check every para

Iterative optimization
Search problem
- We have a parameter space, a cost function, and our job is to search through the space to find the point that minimizes the cost function.
- Since we are using the cost function of squared error, we can think of our job as trying to find the minimum point on an error surface
Error surface
If there is only one parameter, the error surface of a function is a curvy line; if there are two parameters, it’s a bumpy sheet; etc.
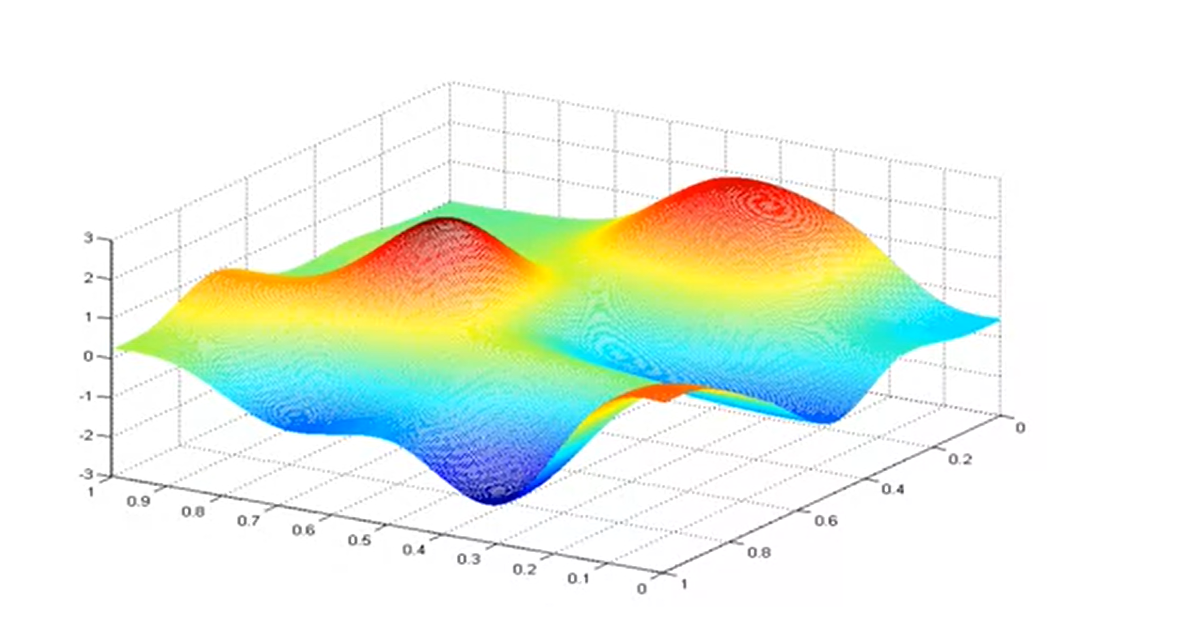
Iterative optimization
To search through a parameter space, we can use local, iterative optimization.
- Start at some point in space (initial seed)
- look at the error surface in a small neighborhood around that point
- move in some directoion in an attempt to reduce the error (cost)
- and repeat until improvements are sufficiently small
Gradient descent
There are many iterative optimazation algorithms out there that vary in how they execute these steps. One simple example is gradient descent

Gradient descent
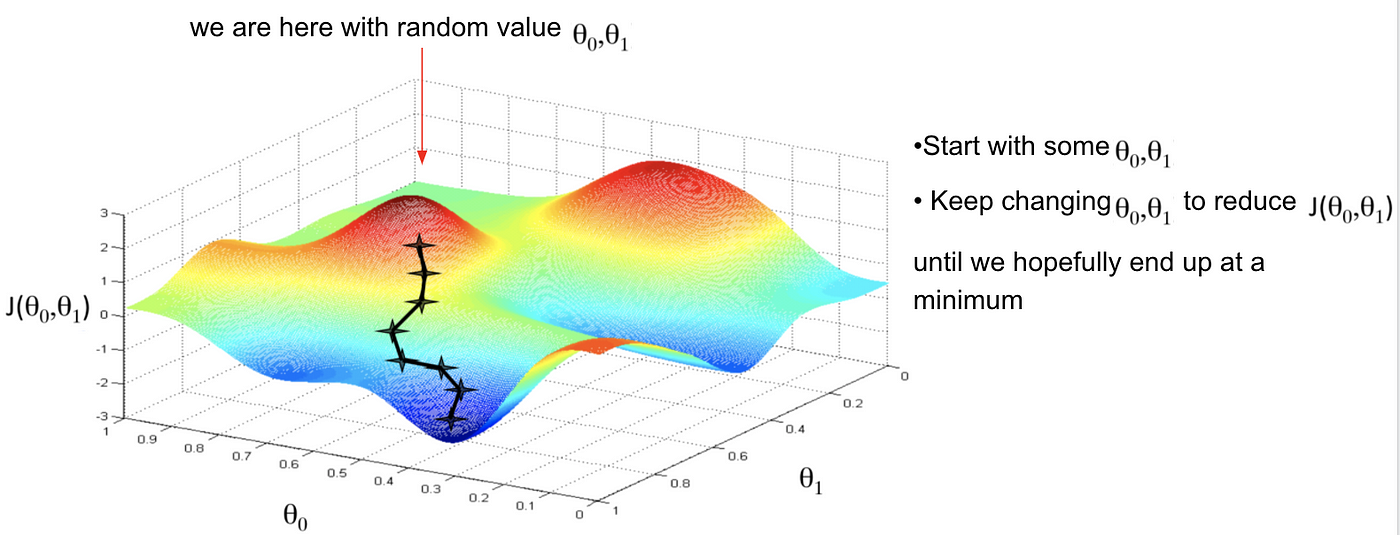
Gradient descent in R
Define our cost function (step 1):
Gradient descent in R
Impliment gradient descent algorithm with optimg (step 2):
Gradient descent v. lm()
We can compare optimg’s estimates to that of lm() to see that they are nearly identical:
Local minumim problem
A potential problem with iterative optimization algorithms is the risk of finding a local minimum.

Local minimum is only relevant for nonlinear models
Only nonlinear models have this potential problem. Even it higher dimensions.
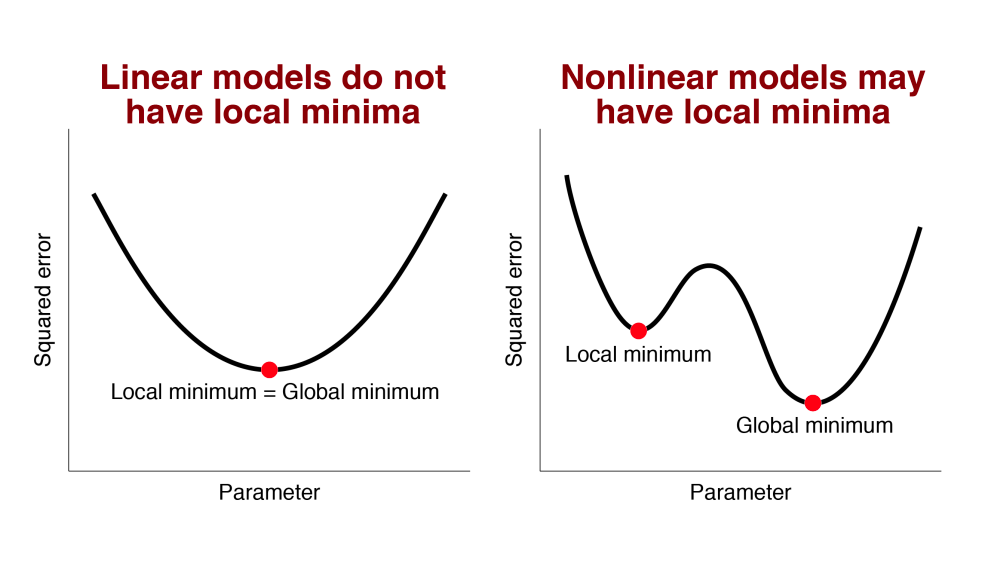
Linear models do not have this problem
For all linear models, we can think of the error surface is being shaped like a bowl, so there is no risk of a local minimum.
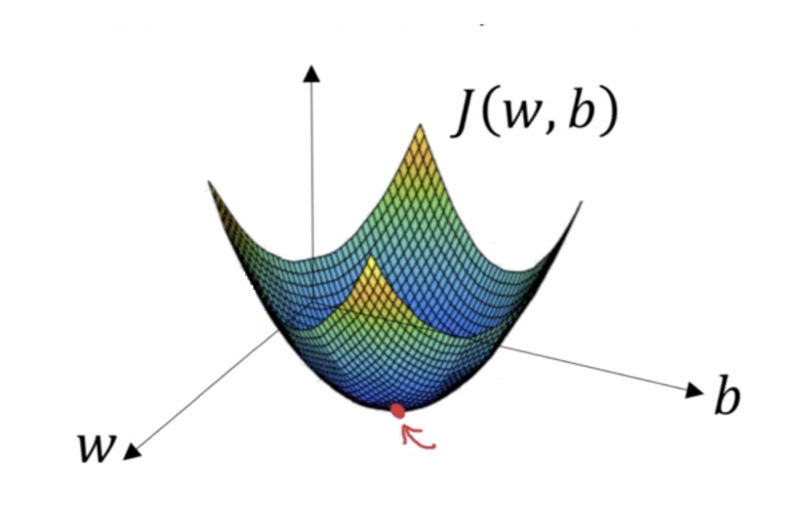
Ordinary least-squares (OLS)
Ordinary least squares solution
Another way we can find the best fitting free parameters for linear (or linearizable nonlinear) models is to use the Ordinary Least-Squares (OLS) estimate.
- In OLS, the best-fitting free parameters are found by solving a system of equations (using matrix operations/linear algebra) which leads to a closed-form solution.
- This means that OLS provides exact values of the best-fitting parameters in one step (as long as a few necessary conditions are met).
OLS v. iterative optimization
- We can contrast this with iterative optimization algorithms (like gradient descent) which gradually adjust the model parameters over multiple iterations to minimize the error, often requiring many steps to converge on approximate values of the best-fitting parameters.
OLS intuition
In OLS, the goal is to model the relationship between input variables and the output variable (\(y\)) as a linear combination. We express this very generally in our favorite equation, where the output (\(y\)) is a weighted sum of inputs (\(x_i\)).
- \(y=\sum_{i=1}^{n}w_ix_i\)
OLS intuition
Recall that this general expression has many 🥸 aliases. That is, the linear model equation can be expressed in many ways, but they are all this same thing:
- in high school algebra: \(y=ax+b\).
- in machine learning: \(y = w_0 + w_1x_1 + w_2x_2 + ... + w_nx_n\)
- in statistics: \(y = β_0 + β_1x_1 + β_2x_2 + ... + β_nx_n + ε\)
- in matrix notation: \(y = Xw + ε\)
OLS on example dataset 1/5
The matrix notation is what allows us to appreciate that we can solve for the best fitting free parameters with linear algebra.
OLS on example dataset 2/5
We can express in matrix notation:
\[ \begin{aligned} \mathbf{y} = \mathbf{X} \mathbf{w} + \mathbf{\epsilon} \end{aligned} \]
Where:
- \(\mathbf{y}\) is the output vector (
rt). - \(\mathbf{X}\) is the input matrix (
experiencewith an intercept). - \(\mathbf{w}\) is the weight vector (parameter estimates including the intercept).
- \(\boldsymbol{\epsilon}\) is the vector of errors (residuals).
OLS on example dataset 2/5
Because our data set is small, we can expand these to help you picture this visually a little better:
- Input Matrix \(\mathbf{X}\) (intercept and
experience):
\[ \begin{aligned} \mathbf{X} = \begin{bmatrix} 1 & 49 \\ 1 & 69 \\ 1 & 89 \\ 1 & 99 \\ 1 & 109 \end{bmatrix} \end{aligned} \]
OLS on example dataset 3/5
- Output Vector, \(\mathbf{y}\) (
rt):
\[ \begin{aligned} \mathbf{y} = \begin{bmatrix} 124 \\ 95 \\ 71 \\ 45 \\ 18 \end{bmatrix} \end{aligned} \]
OLS on example dataset 4/5
- Weight Vector, \(\mathbf{w}\) (Unknown coefficients including intercept):
\[ \begin{aligned} \mathbf{w} = \begin{bmatrix} w_1 \\ % Intercept w_2 % Weight for experience \end{bmatrix} \end{aligned} \]
OLS on example datset 5/5
Putting it all together, the linear model equation becomes, where there is a vector of errors (residuals), \(\mathbf{\epsilon}\).
\[ \begin{aligned} \begin{bmatrix} 124 \\ 95 \\ 71 \\ 45 \\ 18 \end{bmatrix} = \begin{bmatrix} 1 & 49 \\ 1 & 69 \\ 1 & 89 \\ 1 & 99 \\ 1 & 109 \end{bmatrix} \begin{bmatrix} w_1 \\ w_2 \end{bmatrix} + \begin{bmatrix} \epsilon_1 \\ \epsilon_2 \\ \epsilon_3 \\ \epsilon_4 \\ \epsilon_5 \\ \end{bmatrix} \end{aligned} \]
OLS with R example 1/4
At this stage, we can take the mathematicians’ word for it that this provides an exact solution to the best fitting parameter estimates.
We can demonstrate this with code:
OLS with R example 2/4
We need to construct X and Y (must be matrices):
(response_matrix <- data %>% select(rt) %>% as.matrix())
(explanatory_matrix <- data %>% mutate(int = 1) %>% select(int, experience) %>% as.matrix()) rt
[1,] 124
[2,] 95
[3,] 71
[4,] 45
[5,] 18 int experience
[1,] 1 49
[2,] 1 69
[3,] 1 89
[4,] 1 99
[5,] 1 109OLS with R example 3/4
Then we can use our function to generate the OLS solution:
OLS with R example 4/4
Which is exactly the same as that returned by lm() (because lm is doing this!)
Constraints on OLS
- Importantly, if there are more regressors than data points, then there is no OLS solution. The intuition for the underlying math is that if there are more weights than data points, there are infinatly many solutions, all of which acheive zero error.
Constraints on OLS
We can fit if there are fewer inputs than datapoints
data2 <- tibble(
y = c(2, 5, 7),
x = c(1, 2, 3),
z = c(2, 4, 6),
a = c(6, 7, 8)
)
(model1 <- lm(y ~ 1 + x, data = data2))
Call:
lm(formula = y ~ 1 + x, data = data2)
Coefficients:
(Intercept) x
-0.3333 2.5000
Call:
lm(formula = y ~ 1 + x + z + a, data = data2)
Coefficients:
(Intercept) x z a
-0.3333 2.5000 NA NA Constraints on OLS
But not if there are more inputs than datapoints in our model
Call:
lm(formula = y ~ 1 + x + z + a, data = data2)
Coefficients:
(Intercept) x z a
-0.3333 2.5000 NA NA lm() is smart and fits the reduced model it can fit. If we try to solve this the matrix way via our homegrown function, we get an error.
Let’s try it!!
Extra slides
And solve with linear algebra: \(w = (X^TX)^{-1}X^TY\)
Ordinary least squares solution in R
We need to construct X and Y (must be matrices):
(response_matrix <- data %>% select(rt) %>% as.matrix())
(explanatory_matrix <- data %>% mutate(int = 1) %>% select(int, experience) %>% as.matrix()) rt
[1,] 124
[2,] 95
[3,] 71
[4,] 45
[5,] 18 int experience
[1,] 1 49
[2,] 1 69
[3,] 1 89
[4,] 1 99
[5,] 1 109Then we can use our function to generate the OLS solution:
Call:
lm(formula = rt ~ experience, data = data)
Coefficients:
(Intercept) experience
211.271 -1.695