Hypothesis testing
Data Science for Studying Language and the Mind
2024-09-26
Announcements
- Problem set 2 solutions have been posted
- Exam 1 is coming up on Tuesday!
- Practice Exam 1 and solutions posted to website
- Review session Friday 5:15 to 6:45
- Make sure you feel comfortable with the practice exam and all lab questions
- Use the Exam 1 study guide list as a studying checklist
There is a very high probability that I will borrow closely adapted questions from both lab and the practice exam
You are here
Data science with R
- R basics
- Data visualization
- Data wrangling
Stats & Model building
- Sampling distribution
Hypothesis testing- Model specification
- Model fitting
- Model accuracy
- Model reliability
More advanced
- Classification
- Inference for regression
- Mixed-effect models
Explore a more complex dataset
Last week: single quantity
We explored brain volume

This week: two quantities
Brain volume AND sex
Visualize with boxplot
A useful visualization for a categorical variable is a boxplot:

Observed difference in means
Do the two sexes differ in mean brain volume?
Observed difference in means
Sampling variability or true difference in means?

Hypothesis testing framework
3-step process
To determine whether the brains of male and female Penn students differ with respect to the mean, we can use a framework for decision making called hypothesis testing.
- First we pose a null hypothesis that our result is due to nothing but chance (sampling variability)
- Then we ask: if the null hypothesis is true, how likely is our observed pattern of results? This liklihood is the p-value.
- Finally, if the p-value is less some threshold we decide upon (<0.05) then we reject the null hypothesis.
Step 1: Pose the null hypothesis
We pose a null hypothesis for practical reasons: it is the hypothesis for which we can simulate data. We can construct the sampling distribution for a hypothetical world in which our observed value is due to chance (we call this the null distribution).
- To construct the null distribution we can use a process called randomization.
- Randomization is similar to bootstrapping except, on each repeat, we will shuffle the sex and randomly assigning it to each participant.
- This simulates a world in which there is no relationship between brain volume and sex.
Step 1: Pose the null hypothesis

Step 2: How likely is our observed pattern?
If the null hypothesis is true, how likely is our observed pattern of results?
- We can quantify this liklihood directly with the p-value: count the number of values in our null distribution that are more extreme than our observed value and divide that by the number of simulations we generated.
Step 2: How likely is our observed pattern?
Or infer can handle this for us with the get_p_value() function:
# A tibble: 1 × 1
p_value
<dbl>
1 0.242- A large p-value means our observed value is very likely under the null hypotheisis.
- A small p-value means our observed value is very unlikely under the null hypothsis.
Step 2: How likely is our observed pattern?

Step 3: Decide whether to reject
Finally, if the p-value is small enough — less than some threshold we decide upon — we reject the null hypothesis. By convention we consider a p-value less than 0.05 to be implausible enough that we can reject the null hypothesis.

Step 3: Decide whether to reject
Note that obtaining our observed value is implausible under the null, but not impossible. In other words, our decision to reject (or not) could be wrong!
- When we reject a null hypothesis that was actually true, we call it a type I error.
- When we fail to reject a null hypothesis that was actually false, we call it a type II error
Remembering the error types

This figure borrowed from reddit can help you remember the error types. (Null hypothesis here is “NOT pregnant”)
Demo the whole process
There is only one test
There is only one test
If you understand this framework, you can understand any hypothesis test (t-test, chi-squared, etc).

Figure borrowed from Modern Dive textbook
Two ways to simulate data
Remember from last week that there are two ways we can construct a sampling distribution (simulate data):
- Nonparametrically, via brute computational force (simulating many repeats of the same experiment with bootstrapping or randomization)
- Parametrically, by assuming the data were sampled from known probability distribution and working out what happens theoretically under that distribution.
Demo with t-test
Exploring relationships
Visualize with scatter plot
We can explore the relationship between two quantities visually with a scatter plot.

Possible relationships
If there is no relationship between the variables, we say they are independent: knowing the value of one variable provides no information about the other variable.
If there is some relationship between the variables, we can consider two types:
- There may be a linear relationship between the variables. When one goes up the other goes up (positive) or when one goes up the other goes down (negative).
- Or a nonlinear relationship. Nonlinear is a very broad category that encompasses all relationships that are not linear (e.g. a U-shaped curve).
Correlation
Correlation
One way to quantify linear relationships is with correlation (\(r\)). Correlation expresses the linear relationship as a range from -1 to 1, where -1 means the relationship is perfectly negative and 1 means the relationship is perfectly positive.
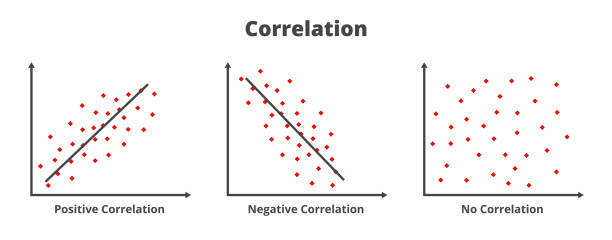
Figure borrowed from iStock photos
Correlation formally
Correlation can be calculated by taking the z-score of each variable (a normalization technique in which we subtract the mean and divide by the standard deviation) and then computing the average product of each variable:
\(r=\frac{\sum_{i=1}^n (\frac{x_i - \bar{x}}{sd(x)})(\frac{y_i - \bar{y}}{sd(y)})}{n}\)
Correlation with R
Or we can use R’s built in correlation function: cor(x,y)
Correlation and sampling variability
Just like the mean — and all other test statistics! — \(r\) is subject to sampling variability. We can indicate our uncertainty around the correlation we observe in the same way we did for the mean last week: construct the sampling distribution of the correlation via bootstrapping and compute a confidence interval.
Correlation and hypothesis testing
How do we test whether the correlation we observed in the data is significantly different from zero? We can use hypothesis testing (as learned today)! Here our null hypothesis that there is no relationship between the variables (they are independent).