Lab 5: Hypothesis testing

Not graded, just practice

Practice your new stats skills with these practice exam questions! Best to open a fresh Google Colab notebook and test things out! Refer to the study guide to find answers as well.

Tip

More than one answer may be correct!

If you would like to practice with a set of data, you can import the following dataset with read_csv. Note that females are coded as NA in this dataset!

# brain volumes simulated from Ritchie et al
"http://kathrynschuler.com/datasets/brain_volume.csv"

1 Visualize a categorical variable

1. Which of the following is the best choice to visualize a categorical variable? Choose one.

   geom_rug() geom_histogram() geom_boxplot() geom_point() geom_smooth()

2. Which of the following figures shows a box plot?

   Rows: 5216 Columns: 2
   ── Column specification ────────────────────────────────────────────────────────
   Delimiter: ","
   chr (1): sex
   dbl (1): volume
   
   ℹ Use `spec()` to retrieve the full column specification for this data.
   ℹ Specify the column types or set `show_col_types = FALSE` to quiet this message.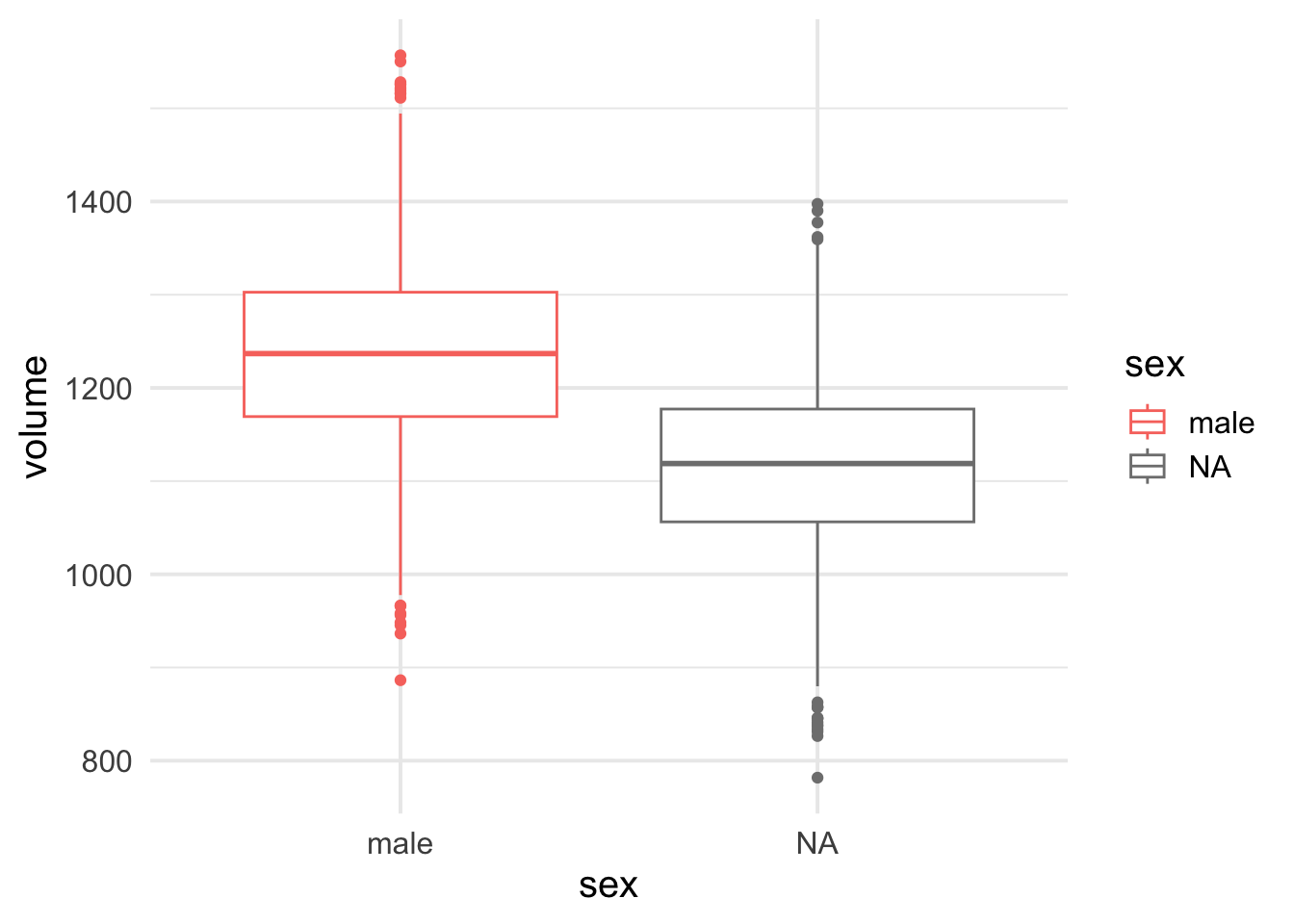

   

   

   left right both the left and right neither the left and right

3. True or false, the difference in means between male and female participants in our sample is subject to sampling variability?

   True False

2 Hypothesis testing framework

1. Fill in the blanks about the 3-step hypothesis testing framework: (1) First we pose a , (2) then we ask if true, how likly is our observed pattern of results? This likelihood is quanitfied with a (), and (3) finally if the liklihood is leass than some thershold, we () the null hypothesis.

2. What is the practical reason we pose a null hypothesis?

   It is the hypothesis most likely to be true. It allows us to generate predictions based on prior beliefs. It is the hypothesis for which we can simulate data. It ensures that the alternative hypothesis is proven false.

3. True or false, Randomization simulates a world in which there is no relationship between brain volume and sex.

   True False

4. Which of the following would compute a p-value?

   Count the number of values in our null distribution that are more extreme than our observed value. Call get_p_value() on an infer object in which we have constructed a null distribution. p-values are not computed. Add up all of the differences in means

5. A large p-value means our observed value is very under the null hypothesis. A small p-value means our observed value is very under the null hypothesis.

6. True or false, a p-value of less than 0.05 indicates obtaining our observed value under the null is impossible

   True False

7. A type I error is also known as a (wrongly thinking that the effect is present); a type II error is also known as a (wrongly thikning the effect is absent)

3 There is only one test

1. There are two ways we can construct a sampling distribution: (1) , via brute computational force; and (2) , by assuming the data were sampled from a known probability distribution.

2. True or false, we can use the t.test() function or assume(distribution = "t") with an infer object to calcuate a p-value for a t-test.

   True False

4 Correlation

1. We can explore the relationship between two quantities visually with a scatter plot. Which geom is best suited for this?

   geom_histogram() geom_boxplot() geom_point() geom_dotplot() geom_density()

2. If there is no relationship between variables, we say they are

3. One way to quantify relationships is with correlation.

4. Correlation ranges from -1 to 1, where:

   -1 means mostly negative and 1 means mostly positive -1 means perfectly negative and 1 means pefectly positive -1 means low correlation and 1 means high correlation

5. True or false, on an infer object, we can calcuate the correlation with calcuate(stat = "correlation")

   True False

6. Suppose we quantify how likely our observed correlation is under the null hypothesis and our p-value is 0.68. Should we reject the null hypothesis?

   Yes No